定点数与浮点数的运算

发表于 更新于 分类于 ，

image-20220119165839638

定点数的加减法运算

  • 整数加法：A[补] + B[补] = [A + B]补
  • 小数加法：A[补] + B[补] = [A + B]补
    运算过程中数值位与符号位一同运算，并将符号位产生的进位自然丢掉，例A=-1100100,B=001101，求A+B
    1
    2
    3
    4
    5
    A[补] = 1,001110
    B[补] = B[原] = 0,001101

    A[补] + B[补] = (A + B)[补] = 1,001110 + 0,001101 =1,011011
    A + B = - 100101
    使用python控制台进行结果的校验：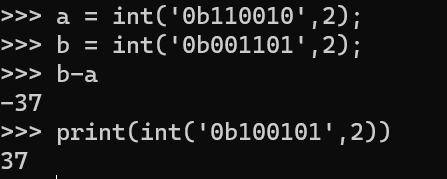
    image-20220124152119279
    再举几个例子，用以熟悉定点数的加减运算：
    例1：A = -10010000，B = -01010000，求A+B
    1
    2
    3
    4
    5
    A[补] = 1,01110000
    B[补] = 1,10110000

    (A + B)[补] = 1,00100000 #丢弃掉符号位的进位
    A + B = - 11100000
    例2：A = -10010000,B = -11010000，求A+B
    1
    2
    3
    4
    5
    A[补] = 1,01110000
    B[补] = 1,00110000

    (A+B)[补] = 0,10100000 # 注意 这里符号位为0 以及是正数了  正数的补码原码反码相同
    A + B = 10100000
    例2中发生了一个现象，即A、B都为负数，相加后却产生了一个正数，原因是两个数都使用8位保存，所以产生了溢出，那么如何判断溢出呢，我们可以约定：
  • 单符号位表示变成双符号位：0 => 00 1 => 11
  • 双符号位产生的进位丢弃
  • 结果的双符号位不同则表示溢出
    上面的约定称为双符号位判断法，使用双符号位判断法重新在来看例2：
    A = -10010000,B = -11010000，求A+B
    1
    2
    3
    4
    5
    6
    A[补] = 1,01110000
    B[补] = 1,00110000

    (A+B)[补] = 11,01110000 + 11,00110000 = 10,10100000
                                            |
                                    双符号位不同，表示溢出
    复习完加法运算，再来看一下定点数的减法运算，定点数减法运算其实是把它的过程转换为加法：
  • 整数减法：A[补] - B[补] = A + (-B)补
  • 小数减法：A[补] - B[补] = A + (-B)补
    其中-B[补]等于B[补]连同符号位按位取反，末位加一，举个例子
    A=11001000，B=-00110100，求A-B：
    1
    2
    3
    4
    5
    A[补] = A[原] = 0,11001000
    B[补] = 1,11001100
    (-B)[补] = 0,00110100

    A[补] - B[补] = A + (-B)[补] = 00,11001000 + 00,00110100 = 00,11111100

浮点数的加减法运算

对于浮点数的加减法运算，主要有一下几个步骤：

  • 对阶，目的是使两个浮点数阶码一致，使得尾数可以进行运算，规则是阶码按小阶看齐大阶的原则
  • 尾数求和
  • 尾数规格化
  • 舍入
  • 溢出判断
    接下来通过一个例子来演示这个过程，设有两个数x、y，其中x=0.1101 * 2^01，y=(-0.1010) * 2^11，并且尾数数值位的存储为4位
阶码符号位 阶码数值位 尾数符号位 尾数数值位
00 0001 00 1101
00 0011 11 1010

第一步，按照对阶的原则，小阶看齐大阶

阶码符号位 阶码数值位 尾数符号位 尾数数值位
00 0011 00 0011（01）
00 0011 11 1010
x = 0.001101 * 2^11，y = (-0.1010) * 2^11，此时由于尾数数值位为四位存储，所以后面的01就被舍弃了
第二步，尾数求和，使用补码进行运算，减法运算转化为加法运算：A - B = A + (-B) 
1
2
3
4
5
6
7
x[原] = 00, 0011
y[原] = 11, 1010

x[补] = 00, 0011
y[补] = 11, 0110

S = (x+y)[补] = 11, 1001

通过第二部，可以得到以下结果：

阶码符号位 阶码数值位 尾数符号位 尾数数值位
00 0011 11 1001

第三步，尾数规格化，对于尾数的规格化需要判断两种情况：

  • S > 0 需要满足：S[补] = 00.1xxxxxx
  • S < 0 需要满足：S[补] = 11.0xxxxxx
    而第二步取得的S = 11,1001即S<0 但是尾数的格式并不满足要求，所以需要进行左移（对应小数点右移），同时阶码相应变化，以满足规格化：
    1
    11, 1001 << 1 = 11, 0010
    左移完后，对应的阶码也需要减1，之前最高位的1被舍弃:
阶码符号位 阶码数值位 尾数符号位 尾数数值位
00 0010 11 0010

所以，S = (x + y)[补] = 11, 0010，而x + y的原码就是(x + y)[原] = - 0.1110，x + y的结果为：-0.1110 * 2^10
第四步 舍入，尾数规格化一般情况下都是左移，但是在特殊情况下可能需要右移，比如发生了溢出，双符号位不一致下，需要右移，右移的话还需要进行舍入操作，舍入操作为”0舍1入”，例：设S补码为10.10110111，此时需要进行右移：

1
2
3
S[补] =  10.10110111 >> = 11.01011011(1) = 11.01011100
                                      |
                                舍弃，1需要进位

右移完成后记得阶码需要+1，还有一种情况是右移完成后还会溢出，例：

1
2
3
4
5
6
S[补] = 01.11111111
第一次右移：01.11111111 >> = 00.11111111(1) >> = 01.00000000
                                        |
                                   舍弃，1需要进位
右移完成后结果：01.00000000，此时需要进行第二次右移
第二次右移：01.00000000 >> = 00.10000000

注意：因为右移了两次，则阶码需要加2

第五步 溢出判断，在定点数运算过程中，双符号位不一致为溢出，而在浮点数的运算过程中，双符号位不一致不算溢出，因为在浮点数的运算过程中，尾数的双符号位可以进行右移，举个例子：x=0.11010011 * 2^1101，y=0.11101110*2^1100
第一步：对阶，小阶向大阶对齐

阶码符号位 阶码数值位 尾数符号位 尾数数值位
00 1101 00 11010011
00 1100 00 11101110 
              |
              ↓
阶码符号位 阶码数值位 尾数符号位 尾数数值位
00 1101 00 11010011
00 1101 00 01110111 
           |              |       |
       阶码加1对齐    尾数右移一位  0被舍去

第二步，尾数求和

1
2
3
4
x 补码=原码=反码= 00.11010011
y 补码=原码=反码= 00.01110111

x + y = 00.11010011 + 00.01110111 = 01.01001010

第三步，规格化，第四步舍入

1
01.01001010 >> = 00.10100101

第五步 溢出判断

阶码符号位 阶码数值位 尾数符号位 尾数数值位
00 1101 00 10100101

阶码符号位一致，没有溢出，则x+y=00.10100101*2^1101

浮点数的乘除法运算

浮点数的乘除法和加减法相似，同样需要经过对阶、尾数求和、尾数规格化、舍入、溢出判断五个步骤，乘法的运算规则为：
阶码相加，尾数求积除法的运算规则为：阶码相减，尾数求商，举个例子简单演示一下，设x = 0.11010011 * 2^1101,y = 0.11101110 * 2^0001，假设阶码4位，尾数8位，计算x * y

1
2
3
x * y = (0.11010011 * 0.11101110) * r^1101+0001 = 11000100*r^1110
                                                         |
                                                    尾数保留八位